Česky 
EnglishFourier Series 3D - interactive demonstration (Discrete Fourier Transform in 3D, FFT)
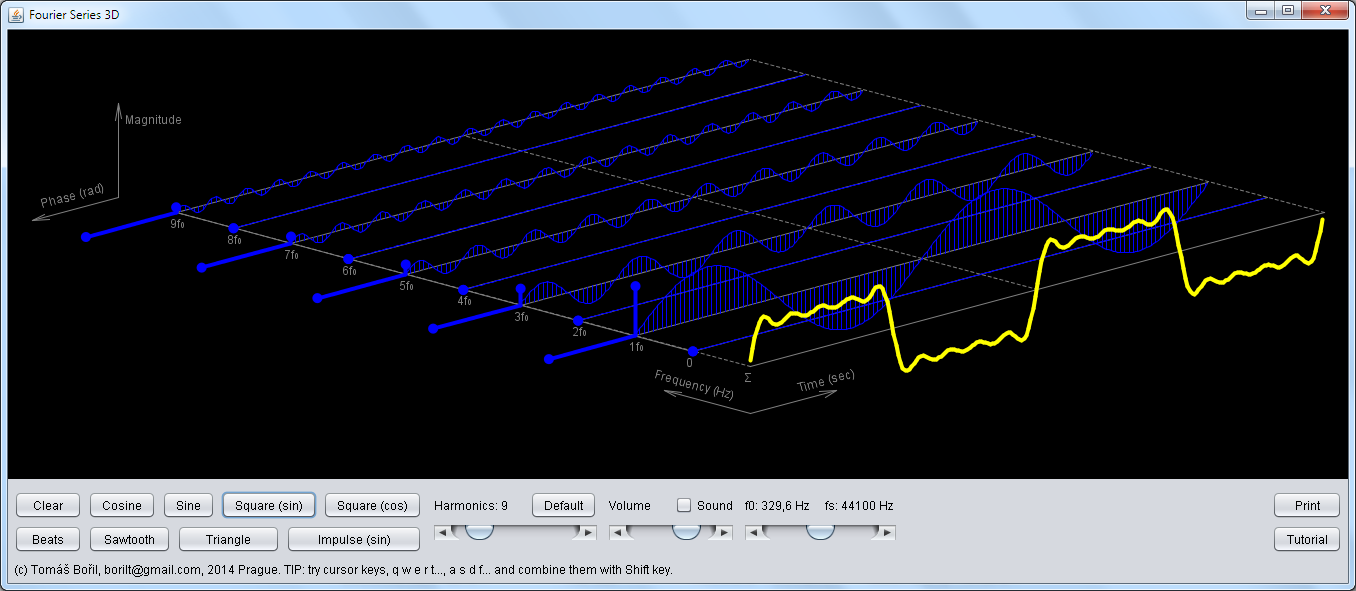
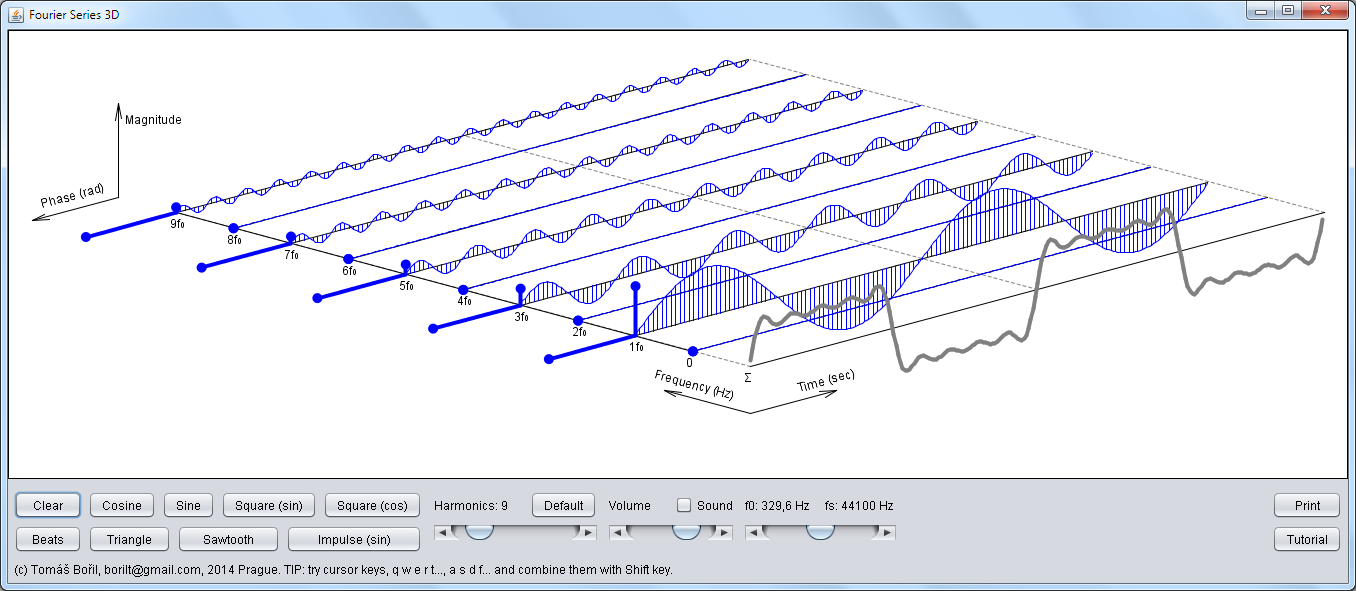Interactive demonstration of Fourier Series in 3D (in fact, it is Discrete Fourier Transform in 3D, FFT). It is easy to understand the connection between time and frequency domain.
All in one 3D picture: time axis, frequency axis, amplitudes, and phases. Everything is interactive - you can drag amplitudes, phases,
draw your own signal, change number of harmonics, turn on sound and listen to the impact of the actions. And more - you can go to the tutorial
section and watch and listen to a lot of interesting commented automatic demonstrations.
Predefined signals: Sine, cosine, square (rectangle), triangle, sawtooth, beats, sine impulse.
Tutorial experiments: Gibbs phenomenon (Gibbs effect), harmonics and sharpness, discontinuity and sharpness, f0 (fundamental frequency), tone color, DC component, frequency response and filtering, sampling theorem, hearing range, phase and perception, beats, make your own instrument, sine impulse (intro to Fourier transform), vowels (synthetic voice), Shepard tone (infinite music scale).
(Runs in browser using HTML5 and JavaScript)
^
Fourier Series 3D - interaktivní demonstrace principu Fourierových řad
Interaktivní demonstrace principu Fourierových řad ve 3D (ve skutečnosti se jedná o diskrétní Fourierovu transformaci ve 3D, FFT). Krásně pochopitelné propojení časové a frekvenční oblasti. V jednom obrázku je časová osa, frekvenční osa, amplitudy a fáze. Vše je navíc interaktivní včetně možnosti zapnout zvuk. Aplikace obsahuje celou řadu zajímavých a detailně komentovaných automatických demonstrací.
Předdefinované signály: sinus, kosinus, obdélník (čvercový průběh), trojúhelník, pila, rázy, sinusový impuls.
Výukové komentované experimenty: Gibbsův jev, harmonické a ostrost, nespojitosti a ostrost, f0 (základní frekvence), barva tónu, stejnosměrná složka (DC), frekvenční charakteristika a filtrace signálů, vzorkovací teorém, rozsah sluchu, vnímání fáze (percepce), rázy, vytvořte si vlastní hudební nástroj, sinusový impuls (úvod k Fourierově transformaci), vokály - samohlásky (syntetický hlas), Shepardova stupnice (nekonečná řada hudebních tónů).
1. Gibbsův jev
Spusť experiment
Čím více harmonických, tím přesnější syntéza signálu. Nicméně musíme počítat s problémem, se kterým ani vysoký počet harmonických nic nesvede. V místech, kde signál obsahuje nespojitost, obdržíme při syntéze harmonickými složkami cca 18% překmitnutí.
U spojitých signálů se tento překmit nesnižuje, ani když se blížíme k nekonečnu harmonických složek, ale dobré je, že šířka (trvání) překmitu je užší a užší. Tím pádem se energie překmitu (a tedy jeho reálný dopad) blíží limitně k nule, a proto nám nakonec prakticky nevadí. Zjednodušeně můžeme tento jev nazvat matematickou hříčkou, nicméně skutečně existuje.
V diskrétních signálech (náš případ) je originální spojitý signál vzorkován v diskrétních časových okamžicích. Proto se může stát, že Gibbsův efekt nezpozorujeme, když se podaří
nastavit fáze takovým způsobem, že se diskrétní časové okamžiky trefí přesně do okamžiků mimo překmity (podívejte se na nastavení fází "rovného" obdélníku, jejich hodnoty jsou mírně posunuty od hodnoty 1/2pi). Musíme si však uvědomit, že toto celé je pouze iluze. Kdybychom si totiž chtěli takový signál poslechnout, musíme ho nejdříve převést zpět do spojité oblasti (a tedy vypočítat i hodnoty mezi diskrétními časovými okamžiky), čímž se Gibbsův efekt opět objeví ("zkráceně: nevidíme ho, ale slyšíme ho...").
Kdybychom si chtěli poslechnout ideální diskrétní obdélník bez Gibbsova efektu (nebo spíše přesněji - s Gibbsovým efektem s nulovou energií), museli bychom nastavit skutečně počet harmonických na nekonečno (neboli použít i nekonečně vysoké frekvenční složky). A z důvodu vzorkovacího teorému vyplývá, že toho můžeme docílit jedině nekonečně vysokou vzorkovací frekvencí - tím jsme se však nechtěně dostali opět ke spojitému signálu... A je také otázkou, zda bychom takto kvalitní obdélník poslechem vůbec ocenili, když slyšíme frekvence do max. 20 kHz. Dá se tedy říct, že žádný člověk ještě nikdy neslyšel ideální obdélníkový zvuk. Kvůli omezenému frekvenčnímu rozsahu sluchu slyšíme vždy jen obdélníky zakulacené...
2. Harmonické a ostrost
Spusť experiment
Přičítání vyšších harmonických je jako přidávání čistých tónů s celočíselným násobkem základní frekvence (nazývané f0 nebo F0).
Čím více vyšších harmonických, tím ostřejší je tvar signálu i jeho zvuk.
Naopak při menším počtu vyšších harmonických je signál zakulacenější a zvuk zní kulatěji (měkčeji, tupěji, temněji).
Přesto ale zůstává základní frekvence (výška tónu) stejná. Vyšší harmonické mění barvu tónu, nikoliv jeho výšku.
Zajímavé je, že při přidávání vyšších harmonických tyto změny vnímáme skutečně jako přidávání nových tónů, po chvíli si na to však
naše ucho zvykne a připadá nám to už spíše jen jako jeden tón s komplexním zabarvením.
3. Nespojitosti a ostrost
Spusť experiment
Pojďme si poslechnout čistý sinusový tón. Zvuk je charakterem velmi tupý a ve spektrální doméně vidíme pouze jednu složku (tzv. spektrální čáru).
Nyní zkuste do signálu nakreslit skok. Okamžitě se to projeví množstvím složek s vysokými frekvencemi, které jsou samozřejmě také slyšet. I jemné oříznutí signálu (tzv. limitace amplitudy) je ihned poznat. Paradoxně může být často velikým problémem tento nejjednodušší čistý signál přehrát. Ačkoliv je matematický předpis jasný, mnoho méně kvalitních reproduktorů není zcela ideálně lineárních a kromě základní sinusovky vygenerují další, sice slabé, ale přesto dobře slyšitelné frekvence, podobné právě např. ořezu amplitud apod. Způsobeno to může být např. ne příliš kvalitním návrhem zvukového zařízení, kdy se vlivem silné přenášené energie rozkmitávají i ty části, které by kmitat neměly (pozorujeme různá chrastění, drnčení, bzučení), nebo zkrátka jen vztah mezi amplitudou vstupního signálu a pohybem membrány reproduktoru není u vyšších hodnot přesně lineární a tvar zvuku tak úplně neodpovídá signálu. Zkrátka, slyšet čistou ideální kulatou sinusovku je poměrně vzácnost.
Námět na další pokus: zkuste v rámci editace signálu nakreslit svoji vlastní sinusovku. Uvidíte, jak je to těžké. Každý malý záchvěv, každá malá odchylka od hladkého harmonického průběhu okamžitě způsobí přítomnost mnoha dalších frekvenčních složek, které jsou poslechem výrazně rozpoznatelné.
Pamatujme si: kulatý signál - kulatý (tupý) tón a pouze nízké frekvence. Ostrý signál - ostrý tón a obsah složek vysokých frekvencí.
Poničení tvaru sinusovky můžeme pozorovat i v případě síťového napájení o základní frekvenci 50 Hz (v některých zemích 60 Hz). Přestože by se mělo ideálně jednat o perfektní harmonické sinusové kmity, zapínání a vypínání různých elektrických spotřebičů tento tvar poničí. Extrémem jsou v této oblasti populární a všudypřítomné spínané zdroje, které silně ovlivňují tvar síťového napájení (tzv. interference), zejména v oblasti frekvencí okolo 25-40 kHz. Problém nastává také ve chvíli, kdy je např. potřeba měřit biologické signály pomocí elektrod (EKG, EEG). Rozvody síťového napájení vyzařují energii (ve formě elektromagnetického vlnění), elektrody fungují jako přijímací anténa a měření bude rušeno relativně silným harmonickým šumem.
4. F0, barva tónu, DC složka
Spusť experiment
Na co má vliv f0, vyšší harmonické a 0 Hz (tzv. stejnosměrná složka)?
Nejprve zkuste přepínat různé předdefinované signály tlačítky dole na liště a poslouchejte jejich zvuk. Barva tónu se mění, ale výška zůstává stejná. Protože vyšší harmonické jsou celočíselným násobkem f0, vzdálenost mezi jednotlivými harmonickými je také f0 (tedy hodnota nejnižší frekvenční čáry, kterou nazýváme základní frekvence). Výška tónu je určena frekvencí f0. Rozdílné amplitudy harmonických pouze mění zabarvení tónu.
A nyní zkusme trik. Přepněte signál na 'pila' a zcela odstraňte čáru f0 (snižte její amplitudu na 0). Samozřejmě, že se změnila barva tónu. Ale co jeho výška? Zkuste měnit frekvenci f0 (posuvníkem či kurzorovými šipkami nahoru a dolů). Stále slyšíte výšku tónu. Vraťte amplitudu f0 na originální hodnotu. Výška tónu se nezměnila, pouze jeho barva. Toto je jeden z triků, kdy si náš mozek domýšlí spoustu věcí. Co je tedy důležité pro odvození základní frekvence? Ve skutečnosti to nemusí být frekvence nejnižší spektrální čáry, ale spíše samotná vzdálenost mezi jednotlivými čárami (která je rovna f0, ať už je samotná f0 v signálu přítomná či ne). Tento jev známe například z pevné telefonní linky. Přenosové pásmo zvuku začíná přibližně na 300 Hz, a přesto vnímáme intonaci mužských hlasů, i když je jejich f0 např. okolo 100 Hz. Anebo jiný příklad, i na levných reproduktorech v notebooku můžeme slyšet melodii basové kytary, přestože základní frekvence tónů jsou pod 80 Hz, což je samozřejmě frekvence daleko mimo rozsah reproduktorů.
A jak je to s komponentou o frekvenci 0 Hz? Má spoustu názvů, např. stejnosměrná složka, D.C. složka (z anglického direct current = stejnosměrný proud, který měl ale fakticky nejen stejný směr (znaménko), ale i konstantní velikost), D.C. komponenta, střední hodnota, průměrná hodnota, konstantní složka, komponenta 0 Hz... Tato složka určuje vertikální posun střední hodnoty signálu. A protože je frekvence 0 Hz (signál konstantní hodnoty) mimo rozsah sluchu 20 Hz - 20 kHz, není vůbec slyšet. Nemá tedy žádný dopad na zvuk.
Je to vždy jen reálné číslo (kladné či záporné), a proto její fáze může nabývat jen diskrétních hodnot (kladné znaménko, záporné znaménko), takže například 0 pro kladné hodnoty a +pi či -pi (což je pro nekonečně periodické signály fakticky totéž) pro záporné hodnoty.
Přestože stejnosměrná složka nemá dopad na vnímaný zvuk, může být v mnoha situacích škodlivá. Například pro některé výpočetní algoritmy, jako je korelace, LPC (lineární prediktivní kódování), PCA (rozklad na hlavní komponenty) apod. Proto se ještě před těmito samotnými algoritmy vždy stejnosměrná složka automaticky odstraňuje. To je naštěstí velice snadné, stačí od každého vzorku signálu odečíst průměrnou hodnotu z celého signálu. Stejnosměrná složka také škodí reproduktorům - jejich membrána je pak neustále vychýlena mimo základní pozici, navíc stejnosměrný proud v tenkých drátcích cívek může způsobit jejich přehřátí, a to i v případě, kdy je zvuk zcela ticho. Proto se stejnosměrná složka odstraňuje v algoritmech pro zpracování zvuku, ve zvukových kartách, dokonce i přímo v zesilovačích u reproduktorů.
Pokud máte ve svém počítači levnou interní zvukovou kartu, můžete v některých případech stejnosměrnou složku objevit např. v záznamech z mikrofonu. Pokud to nastane, jednoduše ji odstraňte před dalším zpracováním signálu. Každý program pro editaci zvuku to umí.
5. Fáze a její vnímání
Spusť experiment
Jaký je dopad různých hodnot fází?
Tvar signálu se změní výrazně, někdy až k nepoznání. Uslyšíme to ale v jednokanálovém (mono) periodickém signálu? Zkuste pohybovat s fázemi a poslouchat.
Na podobný jev můžete narazit při porovnávání zvukových souborů v surovém nekomprimovaném formátu se souborem, který prošel ztrátovou kompresí. Přestože tvar komprimovaného signálu může vypadat výrazně odlišně od originálu, zvukově jsou si velice podobné.
Pokud však budeme zkoumat signály s více kanály (stereo nebo prostorové nahrávky), dopad změn fáze ve spektru bude pravděpodobně zcela odlišný. Podobně důležitý význam mohou mít fáze ve chvíli, kdy signály nejsou stacionárně periodické, fáze má pak vliv na načasování jednotlivých událostí.
6. Vokály
Spusť experiment
Intonace řeči souvisí s frekvencí f0 (způsobenou vibrujícími hlasivkami). Ale co tedy ovlivňuje, že každá samohláska (vokál) zní jinak?
Tzv. kvalita vokálů je určena akustickými rezonancemi vokálního traktu (horizontální i vertikální polohou jazyka, zaokrouhlením rtů apod.)
Tyto rezonanční frekvence nazýváme formanty a díky nim mají některé frekvenční složky vyšší amplitudu než jiné. Formantové frekvence mohou být čteny z amplitudového spektra jako vrcholky pomyslných kopců obepínajících hodnoty jednotlivých harmonických.
V Praatu můžeme zjednodušenou podobu těchto vokálů vygenerovat následujícími příkazy:
Create Sound from formula: "i", 1, 0, 0.1, 44100, "0.5*sin(2*pi*1*300*x) + 0.04*sin(2*pi*2*300*x) + 0.02*sin(2*pi*9*300*x)"
Create Sound from formula: "e", 1, 0, 0.1, 44100, "0.2*sin(2*pi*1*300*x) + 0.3*sin(2*pi*2*300*x) + 0.05*sin(2*pi*3*300*x) + 0.03*sin(2*pi*4*300*x) + 0.04*sin(2*pi*7*300*x) + 0.02*sin(2*pi*8*300*x) + 0.02*sin(2*pi*9*300*x)"
Create Sound from formula: "a", 1, 0, 0.1, 44100, "0.1*sin(2*pi*1*300*x) + 0.1*sin(2*pi*2*300*x) + 0.2*sin(2*pi*3*300*x) + 0.2*sin(2*pi*4*300*x) + 0.07*sin(2*pi*5*300*x) + 0.07*sin(2*pi*6*300*x)"
Create Sound from formula: "o", 1, 0, 0.1, 44100, "0.2*sin(2*pi*1*300*x) + 0.3*sin(2*pi*2*300*x) + 0.2*sin(2*pi*3*300*x) + 0.03*sin(2*pi*4*300*x)"
Create Sound from formula: "u", 1, 0, 0.1, 44100, "0.5*sin(2*pi*1*300*x) + 0.1*sin(2*pi*2*300*x) + 0.01*sin(2*pi*3*300*x)"
7. Namixujte si vlastní nástroj
Spusť experiment
Namixujte si svůj nový hudební nástroj.
Pro změnu f0 využijte řadu kláves A až L, které představují klaviaturu (včetně půltónů ve vyšší řadě). Přidržením klávesy Shift snížíte výšku o jednu oktávu (poloviční frekvence).
Hrajte si melodie a zkoušejte, jak barva tónu zní v různých polohách. Při dlouhém poslechu jednoho tónu byste svůj sluch brzy unavili.
Vylaďte sílu harmonických a jejich počet, anebo začněte se sinusovou vlnou a nakreslete do ní ostré přechody.
Nezapomeňte - vysoké frekvence přidávají do zvuku "pocit blízkosti, živosti", ale nesmíte to přehnat.
Doporučený počet harmonických je 9 až 20. Pro rychlé nastavení na defaultních 9 (např. po kreslení signálu) můžete použít tlačítko 'Výchozí'.
Některé nástroje mohou mít pouze liché harmonické, některé jen sudé, jiné třeba všechny. Některé nástroje znějí dobře v basovém rozsahu, jiné ve středových výškách, další v nejvyšších polohách - experimentujte s f0.
A jako vždy - použijte dobrá sluchátka či reproduktory, abyste si užili celý frekvenční rozsah.
8. Filtr dolní propust
Spusť experiment
Užitečný signál na nízkých frekvencích (v tomto případě pomalá kosinusovka) je rušen složkami na vysokých frekvencích. Ve spektrální doméně je jednoduché toto rušení odfiltrovat.
Ve frekvenční charakteristice filtru (systému, kterým signál prochází) stáhneme na nulu přenos nejvyšších frekvencí tak, aby byly propuštěny jen nízké frekvence (tzv. filtr typu dolní propust).
Jak funguje práce s frekvenční charakteristikou? Při průchodu signálu systémem (filtrem) se násobí spektrum vstupního signálu s hodnotami přenosu frekvenční charakteristiky. Tedy vždy na konkrétní jedné frekvenci se amplituda vstupního signálu vynásobí amplitudou frekvenční charakteristiky na stejné frekvenci, výsledek je amplitudou výstupního signálu. Fáze vstupního signálu jsou posunovány o hodnotu fází frekvenční charakteristiky. Amplitudy se tedy násobí, fáze se sčítají. Pro každou frekvenci zvlášť.
S tímto typem vysokofrekvenčního rušení se setkáváme velice často. Každý kousek drátu se chová jako anténa, takže jsou běžně v signálech patrné složky z různých vysílačů (rádio, mobily, elektrické napájení apod.), dále také ruší zapínání a vypínání různých výkonových spotřebičů, kde rychlý skok v odběru energie vygeneruje rušení na mnoha vysokých frekvencích.
9. Filtr pásmová zádrž
Spusť experiment
Máme vymodelovaný signál, který obsahuje užitečné složky jak na nízkých, tak na vysokých frekvencích. Je ale rušen úzkopásmovou složkou, v tomto případě aditivním harmonickým (sinusovým) rušením. Tento jev můžeme běžně pozorovat například při měření elektrických potenciálů elektrodami, na které se superponuje (přičítá) ruch vyzařovaný z rozvodů síťového napájení (50 nebo 60 Hz dle lokality).
Ve frekvenční doméně je naštěstí velice snadné takovéto úzkopásmové rušení odfiltrovat pouhým snížením amplitud rušivých složek. Protože ve frekvenční charakteristice tlumíme jen úzké pásmo (tento typ filtru se nazývá pásmová zádrž).
Problémem by pochopitelně bylo, pokud by rušivá složka ležela na frekvencích, které jsou i součástí užitečného signálu. V takovém případě bychom filtrací rušivých složek odstranili i část užitečného signálu. Pak je potřeba zvážit, zda je horší rušivou složku ponechat, nebo ji odstranit na úkor užitečného signálu. Případně je možné vyzkoušet pokročilé metody zpracování signálu, které dokáží do určité míry rozpoznat, jak velká část amplitudy náleží užitečné složce a o kolik tedy amplitudu celkově zeslabit, aby byl odstraněn jen nežádoucí ruch.
10. Filtr horní propust
Spusť experiment
Můžeme se také setkat s rušivými složkami na nízkých frekvencí. Například při měření EKG signálu, kde se měří elektrické potenciály vyvolané činností srdce pomocí elektrod umístěných na pokožce lidského těla, jsou určitým problémem pohyby pacienta a jeho pot, což způsobuje změny vodivosti a výsledkem jsou pomalé rušivé složky v naměřeném signálu, jako kdyby signál pomalu "plaval" nahoru a dolů po tzv. izolinii (anglicky isoline drift).
V naší demonstraci jsou užitečným signálem obdélníčkové impulsy (představují např. přenos zprávy zakódované do jedniček a nul), ovšem celý signál je pomalu náhodně unášen nízkofrekvenčním rušením.
Pomocí frekvenční charakteristiky ho odstraníme snadno. Filtr odfiltruje nejnižší frekvence a všechny vyšší frekvence zachová (tzv. filtr typu horní propust).
11. Vzorkovací teorém
Spusť experiment
Pokud chceme propojit diskrétní hodnoty digitálního signálu s reálným světem (například požadujeme přehrát zvuk vzorkovaný v digitálním signálu), musíme říci, kolik vzorků náleží do času jedné sekundy. Tato hodnota se nazývá vzorkovací frekvence (anglicky sample rate, sampling rate nebo sampling frequency) a často se značí fs.
Vzorkovací teorém říká, že vzorkovací frekvence musí být větší než dvojnásobek maximální frekvence obsažené ve spojitém signálu. Pokud nechceme narazit na problém, kterému se říká aliasing, musíme odfiltrovat takové frekvence ze spojitého signálu ještě před vzorkováním. K tomu slouží tzv. anti-aliasingový filtr typu dolní propust.
Aliasing způsobí pomíchání frekvenčních složek v signálu, které jsou mimo rozsah dle vzorkovacího teorému. Fakticky jsou tak zrcadleny do nižších frekvencí uvnitř intervalu 0 až fmax/2. Tohoto jevu si můžeme všimnout u videí, kde je spojitá realita díky snímkům též vzorkována, např. 50 snímky za sekundu. Když je zaznamenán rotující disk kola automobilu, zdá se, že rotace probíhají na nízkých frekvencích nebo dokonce v opačném směru.
V této demonstraci začneme s nízkou hodnotou f0, všechny harmonické jsou v povoleném rozsahu vzorkovacího teorému. Pak začneme zvyšovat f0, přičemž si všimněme, že počet harmonických začne od určité chvíle klesat.
Teoreticky si můžeme hrát s fázemi složek tak, že vytvoříme iluzi obdélníku, který je na obrázku stále perfektně ostrý (počáteční případ našeho obdélníku se 127 harmonickými, ideální obdélník má správně nekonečně harmonických). Ale toto nemá vliv na fakt, že vyšší harmonické ve zvuku (ani signálu) po rekonstrukci do domény spojitého času přítomné nejsou a zvuk zkrátka nezní tak ostrý jako obdélník s větším počtem harmonických. Otázka samozřejmě je, zda tyto frekvence nejsou mimo rozsah našeho sluchu, pak jejich přítomnost či nepřítomnost nevnímáme.
12. Rozsah sluchu
Spusť experiment
Jaký je frekvenční rozsah Vašeho sluchu? Pro tento experiment budete potřebovat tichou místnost a kvalitní sluchátka.
Poslouchejte zvuk a snižujte postupně počet harmonických (můžete i pomocí kurzorových šipek vlevo a vpravo). V kterém okamžiku si povšimnete rozdílu? Zkuste to i v opačném směru - začněte nízkým počtem harmonických a postupně je přidávejte. Kdy přestanete vnímat rozdíly? Obě čísla budou pravděpodobně mírně odlišná jako důsledek psychoakustických jevů (hystereze). Dále můžete počítat s větší z obou hodnot. Konečnou hodnotu lze spočítat jako základní frekvence (f0) krát počet harmonických.
Maximální frekvence sluchového rozsahu klesá s rostoucím věkem. Uvádí se, že děti slyší frekvence zhruba v rozsahu 20 Hz až 20 kHz, starší lidé však mohou mít problém slyšet i 14 kHz. Je to ale vskutku tak závažný problém? Více než čtvrtina je ztracena! Naštěstí vůbec ne. Uvědomme si, že frekvence vnímáme zhruba logaritmicky. To znamená, že vzdálenost intervalu 100-200 Hz je pro nás stejná jako 400-800 Hz. Změna z 20 kHz na 14 kHz je menší než jedna oktáva (oktáva znamená vzdálenost 2x frekvence, je to též rozsah 12 půltónů v hudební chromatické stupnici např. od C do C). Pokud si představíme klaviaturu koncertního klavíru, pak tato změna je relativně jako přijít o posledních 5 bílých kláves.
Ve skutečnosti však skutečný koncertní klavír končí na mnohem nižších frekvencích - poslední tón bývá většinou C8 s frekvencí okolo 4190 Hz (záleží na způsobu ladění). Frekvenční rozsah základních frekvencí tónů v hudbě nebývá o mnoho vyšší (i nejvyšší tón na malé pikole nejde výše), takže se nemusíme ve stáří obávat ztráty schopnosti slyšet hudební tóny. Změna díky omezenému frekvenčnímu rozsahu nastane pouze ve vnímání vyšších harmonických těchto tónů, a tedy barvy tónů. Nicméně lidský mozek dokáže velmi dobře kompenzovat pomalu probíhající změny, takže si pravděpodobně nevšimnete ničeho zvláštního, pokud vyloženě nebudete experimentovat s měřením frekvenčního rozsahu objektivními specializovanými metodami.
Prosíme však, neberte toto konkrétní měření příliš vážně. Amplituda harmonických obdélníkového signálu velice rychle klesá s rostoucími frekvencemi, takže je vysoce možné, že důvod, proč změny neslyšíte, není Vaším skutečným frekvenčním rozsahem, ale spíše tím, že amplituda složek vyšších frekvencí v tomto experimentu je již příliš nízká. Smyslem této demonstrace je spíše ukázat dopad na barvu tónu při ztrátě vyšších harmonických.
13. Zázněje (rázy)
Spusť experiment
Pokud máme dvě velice blízké frekvence, vnímáme je jako jeden tón s periodickým kolísáním hlasitosti (tzv. rázy).
Výslednou vnímanou frekvenci vypočteme jako průměr obou původních frekvencí.
Frekvence periodického kolísání hlasitosti je rovna rozdílu obou původních frekvencí.
Uvažujme příklad se dvěma tóny o frekvencích 439 Hz (referenční tón) a 441 Hz (měřený tón). Poslechem vnímáme jen jeden tón, a sice s frekvencí 440 Hz a kolísáním hlasitosti o frekvenci 2 Hz (perioda 0,5 sekundy).
Hudebníci velice často využívají tento precizní způsob měření pro kontrolu ladění dvou shodných tónů, oktáv a dalších jednoduchých intervalů.
Měření pomocí rázů nalezneme ale i v jiných oblastech. Jedná se o nejpřesnější způsob měření, které má k dispozici fyzika. Pokud měříme efekt interference dvou vlnění velice blízkých frekvencí, obdržíme velmi dlouhé (ale jednoduše měřitelné) periody. Uveďme příklad, kdy byla změřena frekvence přechodu stavů ve struktuře rubidia s rozlišením menším než 10^-16 (porovnávalo se s referencí více než 50 dnů). Z tohoto důvodu jsou některé jednotky SI odvozeny od času či frekvence (například 1 metr je vzdálenost, kterou urazí světlo ve vakuu během 1/299 792 458 sekundy).
V případě naší ukázky se zvukem jsme si dovolili malý trik, protože nebylo možné nastavit tak malý rozdíl frekvencí pomocí standardních hodnot na osách obrázku. Proto to, co slyšíte, neodpovídá přímo hodnotám uvedeným na osách. Slyšíte skutečně výše popisovaných 439 Hz a 441 Hz. I nakreslený průběh signálu je potřeba brát pouze ilustračně, ve skutečnosti je během jedné "zázněje" mnohem více period, než je zobrazeno.
14. Od impulsu k Fourierově transformaci
Spusť experiment
Zaměřme se na jednoduchý sinusový impuls. Jak je možné namíchat signál, který někde začíná a někde končí, tedy má omezené trvání, jen pomocí nekonečně dlouhých periodických harmonických kmitů?
Lze tak učinit pomocí mnoha harmonických funkcí s blízkými frekvencemi a jemně vyladěnými fázemi, nastane tím efekt podobný rázům (kde se signál také objevuje a mizí).
Zkuste jenom trochu pohnout s fází některé ze složek a uvidíte, jak perfektně jsou vyváženy, abychom v součtu obdrželi nulový signál před začátkem impulsu.
Pomocí této demonstrace máme nakročeno k vysvětlení tzv. Fourierovy transformace - nástroji podobnému Fourierovým řadám, ale navrženému pro modelování jednorázových neperiodických impulsů. Použitím Fourierovy transformace můžeme syntetizovat impulsy, které začnou v nějakém časovém okamžiku a končí třeba o pár okamžiků později. A mimo tento interval jsou zcela nulové. A i takovýto signál je přitom modelován nekonečně dlouhými periodickými sinusovými vlnami. Trik spočívá v tom, že frekvenční složky jsou tak blízko sebe, že jsou schopny vymodelovat něco velice podobného "rázům", které vidíme v této demonstraci, a díky tomu pak můžeme obdržet velice dlouhý signál nulové hodnoty. Ve skutečnosti je to potom tak, že vzdálenosti mezi sousedními frekvencemi ve spektru začínají být nekonečně jemné a úseky s nulovou hodnotou klidně i nekonečně dlouhé.
Fourierovy řady modelují periodické signály a výsledkem je diskrétní spektrum (frekvence f0 a její celočíselné násobky). Oproti tomu Fourierova transformace modeluje signály impulsního charakteru a výsledkem je spojité spektrum s hodnotami frekvencí v oboru reálných čísel.
15. Shepardova stupnice
Spusť experiment
Jedná se o nekonečně rostoucí chromatickou stupnici. Nejdříve jen poslouchejte zvuk a nedívejte se na obrazovku, ať není zvukový vjem rozptylován obrazovými informacemi. V tomto případě Vám nebudeme kouzlo prozrazovat, vysvětlení tajemné magie si musíte odhalit sami :-)
License
License: MIT
Copyright (c) 2016 Tomáš Bořil, borilt@gmail.com
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the “Software”), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED “AS IS”, WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.